平均値の定理についての考察

高校数学の内容に「平均値の定理」があります。平均値の定理は、大学で解析学を学ぶときの基礎となる定理ですが、受験ではあまり活躍せず、定理の意味についてもほとんど語られないまま高等教育を終える方もいらっしゃると思います。 今回はそんな平均値の定理についてお話ししたいと思います。

1 ラグランジュの平均値の定理

実は平均値の定理にはいくつかのバリエーションがあるのですが、単に「平均値の定理」というと、以下のラグランジュの平均値の定理を指します。

さて、この定理の意味するところですが、何が平均値なのでしょうか？
平均値というと、いくつかの数値を足し合わせて全体で割った値といういメージですが、式(1)はそのような計算をしておらず、条件に当てはまる点の存在を主張するものとなっています。

インターネットで平均値の定理の意味を調べてみると、「閉区間 \([a,b]\)における平均の変化率\(\frac{f(b)-f(a)}{b-a}\)と、瞬間の変化率\(f'(c)\)が等しい点\(c\)が存在する」という説明がなされていました。この説明も正しいのですが、ここではもう少し解像度を上げて、次のように述べたいと思います。

この表現では、条件に当てはまる点の存在を主張するだけでなく、その点における\(f'(c)\)の値が\(f'(x)\)の平均値であると主張しています。果たしてこの表現が妥当なのか見ていきましょう。

微分と積分の関係式より、

\[\begin{align}
f(b)-f(a)=\int_a^b f'(x) \ dx \\
\frac{f(b)-f(a)}{b-a}=\frac{1}{b-a} \int_a^b f'(x) \ dx \ .
\end{align}\]
ここで右辺が何を表しているか考えてみましょう。 まずは直感的な説明として、\(\int_a^b f'(x) \ dx\)は\(f'(x)\)の値を\(a\)から\(b\)まで足し合わせたものに相当します。それを、足し合わせた区間である\((b-a)\)で割っているので、右辺は\([a,b]\)における\(f'(x)\)の平均値であると言えます。

もう少しちゃんと説明しましょう。高校の教科書に習って話すなら、\(\int_a^b f'(x) \ dx\)は\(f'(x)\)と\(x\)軸、\(x=a, x=b\)で囲まれた領域の面積です。この領域と面積が等しく、底辺も等しい長方形を考えます（図1）。

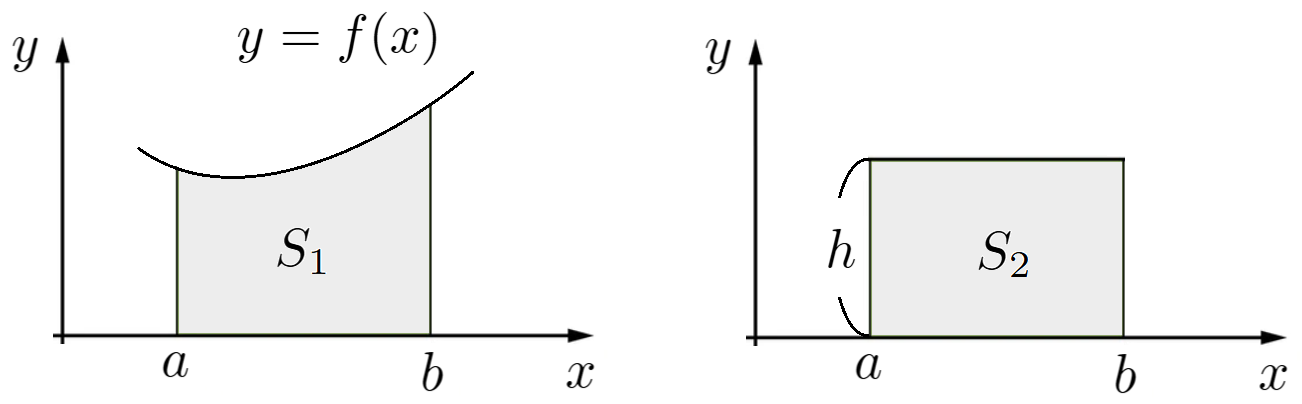
面積と底辺が等しいということは違いがあるのは高さだけです。図1の左の図形の高さは\(f'(x)\)の値であり、それを平均化したものが右の図形となります。右の図形の高さを\(h\)とすると、

\[\begin{align}
S_2=(b-a) \cdot h \\
h=\frac{S_2}{b-a} \ .
\end{align}\]
\(S_2=S_1=\int_a^b f'(x) \ dx\)なので、

\[\begin{align}
h&=\frac{1}{b-a} \int_a^b f'(x) \ dx \\
&=\frac{f(b)-f(a)}{b-a}
\end{align}\]
となります。\(h\)は\(f'(x)\)の値を平均化したものなので、\(\frac{f(b)-f(a)}{b-a}\)は\(f'(x)\)の平均値と言えます。 また、本来の主張である点\(c\)の存在についても、\(f'(c)=\)(平均値)となる点の存在を証明することができます。（厳密な証明は大学レベルとなりますのでその点はご了承ください。）

\(f'(x)\)は\([a,b]\)で連続であるから、最小値と最大値が存在する（最大値の原理）。 (最小値) \(\leq\) (平均値) \(\leq\) (最大値)であり、等号が成立するのは(最大値) = (最小値)の場合、すなわち\(f'(x)\)が定数関数の場合である。このとき、(最大値) = (最小値) = (平均値)なので\(f'(x)\)は\((a,b)\)上の任意の点\(c\)で\(f'(c)=\) (平均値)となる。

次に(最小値) \(<\) (最大値)の場合を考える。最小値を\(f'(p)\)、最大値を\(f'(q)\)とすると、\(f'(p) < f'(q)\)であるから中間値の定理より、閉区間\([f'(p),f'(q)]\)内の任意の点\(r\)に対して、\(f'(c)=r \ (p \leq c \leq q)\)となる点\(c\)が存在する。(平均値) \(\neq\) (最小値), (平均値) \(\neq\) (最大値)なので、\(c \neq p, \ c \neq q\)である。よって\((a,b)\)上に\(f'(c)=\) (平均値)となる点\(c\)が存在する。
このように平均値の存在と、

\[\begin{align}
f'(c)=(\mbox{平均値})=\frac{f(b)-f(a)}{b-a}
\end{align}\]
となるような点\(c\)の存在が保証されます。これが平均値の定理の意味と言えるでしょう。

ここまでの議論で、平均値の定理は平均値の存在を保証する定理であることを述べてきましたが、式(2)は、\(f(x)\)の変化率（微分）の平均値が閉区間の両端の変化率に等しいことを表しています。これは直感的には意外なことです。というのも、\(f(x)\)の分布が極端に偏っている場合、その影響で\(f(x)\)全体の平均値が引き上げられてしまいますが、\(f'(x)\)の平均値は閉区間の両端の値から求めることができるからです。この方法を応用すれば、\(f'(x)\)の平均値だけではなく\(f(x)\)の平均値を求めることもできます。

2 積分における平均値の定理

式(3)において\(f'(x)\)を\(f(x)\)に変えると、

\[\begin{align}
\frac{F(b)-F(a)}{b-a}=\frac{1}{b-a} \int_a^b f(x) \ dx
\end{align}\]
となります。ここで、\(F(x)\)は\(f(x)\)の原始関数です。式(3)を特に「積分における平均値の定理」と呼びます。 前節の内容を踏まえると、式(3)の右辺は\(f(x)\)の平均値であり、それを左辺のように計算できるというわけです。
せっかくなので計算してみましょう。簡単な例として、\(f(x)\)が一次関数の場合を考えます。\(f(x)=\alpha x+\beta\)と置いて、\([a,b]\)における平均値を計算します。 一次関数は値が一定の割合で変化するので、平均値は閉区間の中間である\(f(\frac{a+b}{2})\)となります。よって平均値は、

\[\begin{align}
f\left(\frac{a+b}{2}\right)=\frac{\alpha}{2}(a+b)+\beta \ .
\end{align}\]
次に、積分における平均値の定理を使って\(f(x)\)の平均値を計算します。原始関数を求める必要がありますが、定積分なので積分定数は省略して、

\[\begin{align}
F(x)=\frac{\alpha}{2}x^2+\beta x \ .
\end{align}\] 式(3)より平均値は、

\[\begin{align}
\frac{F(b)-F(a)}{b-a} &= \frac{1}{b-a} \left(\frac{\alpha}{2}(b^2-a^2)+\beta (b-a)\right) \nonumber \\
&= \frac{\alpha}{2}(a+b)+\beta \ .
\end{align}\]
式(4)と一致していることがわかります。この例ではわざわざ平均値の定理を使う必要はありませんが、より高度な関数になると古典的な方法では平均値を求められない場合があり、そんなときに平均値の定理が活用できます。
もう少しレベルを上げて、\(f(x)={\rm sin} x \ (0 \leq x \leq \pi)\)の平均値を計算してみましょう。この定義域では\(0 \leq {\rm sin} x \leq 1\)なので中間の値は1/2ですが、\(\frac{\pi}{6} \leq x \leq \frac{5\pi}{6}\)のとき\(\frac{1}{2} \leq {\rm sin} x\)なので、この関数は1/2より大きい値をとる区間の方が広く、平均値も 1/2 より大きい値をとることが予想できます。

積分定数を省略すると\(F(x)=-{\rm cos} x\)となるので、式(3)を用いて、

\[\begin{align}
\frac{F(\pi)-F(0)}{\pi-0} &= \frac{1}{\pi} (-{\rm cos} \pi +{\rm cos} 0) \\
&= \frac{2}{\pi} \\
&= 0.6366 \cdots \ .
\end{align}\] 実際に1/2より大きい値をとることがわかりました。
まとめると、平均値の定理は、閉区間における連続関数の平均値の存在を保証し、平均値を計算することができます。また、\(f(x)\)の平均値は原始関数\(F(x)\)の閉区間における両端の値で決まることもわかりました。